Homework #2

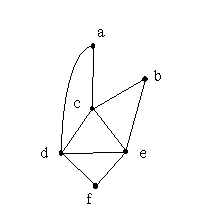
1. Given the following graph:

a) write down all breadth-first traversals that start at vertex b (10 points)
b) write down all depth-first traversals that start at vertex e. (10 points)

2. Using the graph in problem 1, decide whether there is an Euler circuit in the graph or not. If you decide there is one, then find it by using Fleury's algorithm; show your work. (20 points)

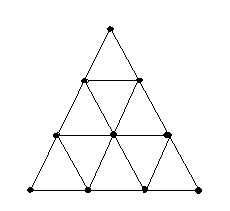
3. The graph below is continued towards the bottom to an arbitrary, finite depth. Does the graph contain an Euler cycle? If yes, then describe one. (10 points)

4. Let A = {1, 2, 3, 4, 8} and a relation R defined as: aRb if and only if a*b<10

a) write down the set representation of R
b) what is the matrix representation of R?
c) draw the digraph of R
d) is there any source in the digraph?
e) is there any sink in the digraph?
f) find a path of length 3 between vertices 1 and 3
g) find a circuit in the digraph.

Each part of this problem is worth 5 points.

5. Represent the relation in problem 4 as a graph (ignore in other words the arrows on the digraph's edges):

a) write down the degree of each vertex.
b) is there a bridge in the graph?
c) is there a Hamiltonian path? If yes, find one.
d) is there a Hamiltonian circuit in the graph? If yes, find one.

Each part of this problem is worth 5 points.

5. Assume the following graph which describes the structure of a communications network between some cities (labeled from A to J):

The cost (in millions of dollars) of upgrading connections between two directly connected cities is given in the table below:

       A    B    C    D    E    F    G    H    I    J
  ==|=================================================
  A |      2.6                      2.7  2.1
  B | 2.6       4.2                      3.6  3.3  2.9
  C |      4.2       4.4                           2.2
  D |           4.4                           2.5  2.0
  E |                          1.7            3.3  5.3
  F |                     1.7       3.4  1.8
  G | 2.7                      3.4       2.4
  H | 2.1  3.6                 1.8  2.4       2.8
  I |      3.3       2.5  3.3            2.8
  J |      2.9  2.2  2.0  5.3  
  --|-------------------------------------------------

In the beginning the company that runs the network wants to do an upgrade that reaches every city at the minimum cost. Find out what links must be upgraded an what is the cost of the upgrade. (25 points)

6. Given the following expression a*b*(c/d) - (a+b*c)

a) draw a picture of the tree representation of this expression (5 points)
b) write down the tuple representation of the tree (5 points)

Maximum mark: 140 (100%)