


Next: Nondeterministic Finite Automata
Up: Automata
Previous: Automata
A deterministic finite accepter or dfa 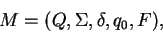 is defined as quintuple
is defined as quintuple
where
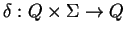 is a finite set of internal states.
is a finite set of internal states.
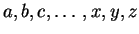 is a finite set of symbols, called input alphabet.
is a finite set of symbols, called input alphabet.
-
 is
a total function called the transition function.
is
a total function called the transition function.
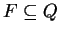 is the initial state.
is the initial state.
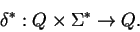 is a set of final states.
is a set of final states.
It is convenient to introduce the extended transition function
The second argument of 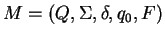 is a string rather than a single symbol, and
its value gives the state the automaton will be in after reading that
string.
The language accepted by a dfa
is a string rather than a single symbol, and
its value gives the state the automaton will be in after reading that
string.
The language accepted by a dfa
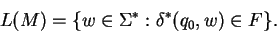 is the set of all strings on
is the set of all strings on 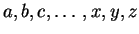 accepted by
accepted by 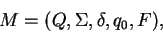 .
Formally,
.
Formally,
xiangyang li
2000-09-06