


Next: Proof by Contradiction
Up: Proof Techniques
Previous: Proof Techniques
Induction is a technique by which the truth of a number of statements can be
inferred from the truth of a few specific instances.
Suppose that we want to prove a sequence of statements
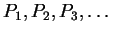 to be true; or we want to prove a statement is true for a sequence of instances.
Suppose that the following conditions holds:
to be true; or we want to prove a statement is true for a sequence of instances.
Suppose that the following conditions holds:
- For some
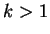 , we know that
, we know that
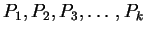 are true.
are true.
- For any
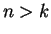 , the truths of
, the truths of
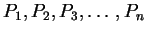 imply the truth
of
imply the truth
of 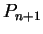 .
.
We then use induction to show that every statement in the sequence is true.
The first condition of the induction is called basis, and the second condition
is called the inductive step, which is usually the major step in the proofs by
induction.
xiangyang li
2000-09-06