


Next: Operations on Alphabet, Languages,
Up: Review
Previous: Proof by Contradiction
Some terminologies used in this course include the follws.
For more, please see the textbook from page 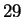 to page
to page  .
.
- Alphabet:
- It is finite set of symbols, often denoted by
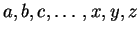 .
For example, the alphabet of English is
.
For example, the alphabet of English is
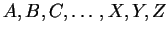 , and
, and
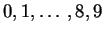 , punctuation, space and number digits
, punctuation, space and number digits
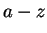 .
For the sake of convenience, we often use
.
For the sake of convenience, we often use 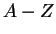 to denote the alphabets
to denote the alphabets
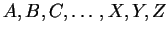 . Similarly to use
. Similarly to use 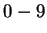 to denote
all capital English alphabets, use
to denote
all capital English alphabets, use 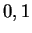 to denote all decimal digits.
For computer, the alphabets are often binary
to denote all decimal digits.
For computer, the alphabets are often binary 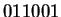 .
.
- String:
- It is finite sequence of symbols taken from alphabet
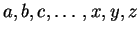 .
For example, in English: Hello world.
A sequence of binary bits
.
For example, in English: Hello world.
A sequence of binary bits 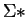 is a string.
Notice that the set of all strings is denoted by
is a string.
Notice that the set of all strings is denoted by 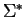 .
For example,
.
For example,
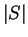 .
It is countably infinite.
.
It is countably infinite.
- Language:
- It is set of strings, i.e., subset of
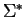 .
distinguishing strings into those in/out of the language
.
distinguishing strings into those in/out of the language
- Machine:
- It is formal abstraction of a computer
based on states and transitions between states.
It computes some output from input.
Typically, there are three uses of machine, which can be related to each
other.
- acceptance:
- input = string, output = yes/no membership in language
- enumeration:
- input = nothing, output = all strings in language
- function:
- input = string, output = string
- Grammar:
- The rules for deriving and parsing strings,
akin to high school grammar rules for natural languages.
- Expression:
- A meta-string that "denotes" a language.
Subsections



Next: Operations on Alphabet, Languages,
Up: Review
Previous: Proof by Contradiction
xiangyang li
2000-09-06