Nondeterministic finite state machine or nondeterministic finite automaton (NFA) is a finite state machine where for each pair of state and input symbol there may be several possible next states. This distinguishes it from the deterministic finite automaton (DFA), where the next possible state is uniquely determined. Although the DFA and NFA have distinct definitions, it may be shown in the formal theory that they are equivalent, in that, for any given NFA, one may construct an equivalent DFA, and vice-versa: this is the powerset construction. Both types of automata recognize only regular languages.

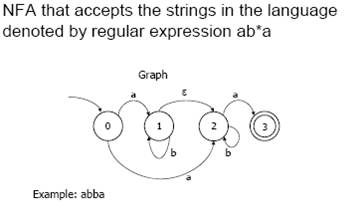
An extension of the NFA is the NFA-lambda (also known as NFA-epsilon or the NFA with epsilon moves), which allows a transformation to a new state without consuming any input symbols.

For example, if it is in state 1, with the next input symbol an a, it can move to state 2 without consuming any input symbols, and thus there is an ambiguity: is the system in state 1, or state 2, before consuming the letter a? Because of this ambiguity, it is more convenient to talk of the set of possible states the system may be in.

Thus, before consuming letter a, the NFA-epsilon may be in any one of the states out of the set {1,2}. Equivalently, one may imagine that the NFA is in state 1 and 2 'at the same time': and this gives an informal hint of the powerset construction: the DFA equivalent to an NFA is defined as the one that is in the state q={1,2}. Transformations to new states without consuming an input symbol are called lambda transitions or epsilon transitions. They are usually labeled with the Greek letter λ or ε.

The notion of accepting an input is similar to that for the DFA. When the last input symbol is consumed, the NFA accepts if and only if there is some set of transitions that will take it to an accepting state. Equivalently, it rejects, if, no matter what transitions are applied, it would not end in an accepting state.

In general, NFA can have ε transitions and missing transitions for any given input symbol.

NFA is formally represented by the 5-tuple 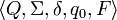, where:

Q is a set of states.

Σ is a finite set of symbols, that we will call the alphabet of the language the automaton accepts.

δ is the state transition function

(δ : Q × (Σ U { ε} -> Q)

q0 is the initial state

F is the set of final states, subset of S