


Next: Relations
Up: Review
Previous: Review
Let 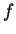 be a function defined on a set
be a function defined on a set 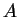 and taking values in a set
and taking values in a set 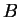 .
Set
.
Set 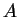 is called the domain of
is called the domain of 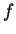 ; set
; set 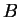 is called the range of
is called the range of 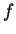 .
Function
.
Function 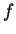 is said to be one-to-one
(i.e., an injection or embedding) if, whenever
is said to be one-to-one
(i.e., an injection or embedding) if, whenever
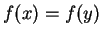 , it must be the case that
, it must be the case that 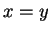 .
In other words,
.
In other words, 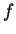 is one-to-one if it maps distinct objects to distinct
objects.
Function
is one-to-one if it maps distinct objects to distinct
objects.
Function 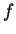 is said to be onto (a.k.a. a surjection) if, for any
is said to be onto (a.k.a. a surjection) if, for any 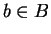 ,
there exists an
,
there exists an 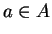 for which
for which 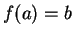 .
A function is bijection if it is one to one
(i.e., injection) and onto (i.e., surjection).
If function
.
A function is bijection if it is one to one
(i.e., injection) and onto (i.e., surjection).
If function 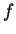 is defined for each element of
is defined for each element of 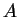 ,
then
,
then 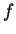 is said to be a total function;
otherwise,
is said to be a total function;
otherwise, 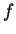 is said to be a partial function.
is said to be a partial function.
xiangyang li
2000-09-06