


Next: Countably Sets
Up: Review
Previous: Functions
A relation on a set 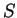 is a set of ordered pairs of elements from
is a set of ordered pairs of elements from 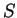 .
Therefore, the relation is a subset of
.
Therefore, the relation is a subset of 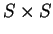 .
An equivalence relation on a set
.
An equivalence relation on a set 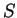 is a relation
is a relation 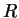 satisfying certain properties.
Write
satisfying certain properties.
Write 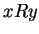 to mean
to mean 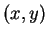 is an element of
is an element of 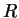 ,
and we say
,
and we say 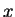 is related to
is related to 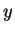 , then the properties are
, then the properties are
- Reflexive:
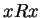 for all
for all 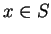 ,
,
- Symmetric:
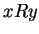 implies
implies 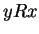 for all
for all 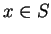 and
and 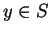 .
.
- Transitive:
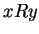 and
and 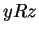 imply
imply 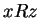 for all
for all 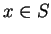 ,
, 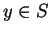 and
and 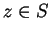 .
.
Where these three properties are completely independent.
Other notations are also often used to indicate a relation,
e.g., 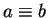 or
or 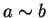 .
Good reference for set theory: http://mathworld.wolfram.com/Set.html
.
Good reference for set theory: http://mathworld.wolfram.com/Set.html
xiangyang li
2000-09-06